Why do we need to calculate state of charge?
The ability to identify where energy is available in the network and where energy is needed is a key step toward achieving this goal, and in order to accomplish this we need an accurate measurement of battery state of charge. Battery state of charge (SoC) is the proportion of capacity available relative to the battery’s full capacity. SoC data enables our networks to actively redistribute power when there is risk of blackout and maintain more balanced levels of charge, ultimately forming the foundation of the future grid optimizations and predictive models in our tech pipeline.
SoC data plays a vital role in allowing energy to be distributed intelligently in our mesh-grid networks.
Why is this a difficult problem?
Initially, I was surprised to find so much academic work on SoC estimation, with methods varying greatly in degrees of complexity and of success. Every piece of technology we own confidently reports SoC, and we accept it as truth. But what about that time I called an Uber to the airport with my phone at “40 %” only for it to die immediately, or that old laptop that would hang on at “1%” for hours? In fact, it is challenging to estimate SoC because it cannot be measured directly from a battery under load (or recently under load), and so we need to design an algorithm to extract SoC from the measurements available.

Sometimes charging electronics gets more complicated than we want it to be…
What are the options?
Fundamentally, SoC is estimated from battery current and voltage measurements. There are three main ways to do this: 1. Coulomb counting, 2. model-based approach, and 3. data-driven approach. The methods differ in their performance and complexity, making them each a good fit for particular applications.
Coulomb counting
Coulomb counting is the simplest option. It counts up the current entering and exiting the battery over the course of time. While this is effective for short time intervals, small errors rapidly accumulate, leading to an SoC estimate that diverges from the truth over time, as seen in the figure below. As a result, frequent recalibration to known SoC levels is required in order for a Coulomb counter to perform reliably. Additionally, the algorithm requires the initial SoC to be set precisely, and it cannot recover from data lapses until it is recalibrated.
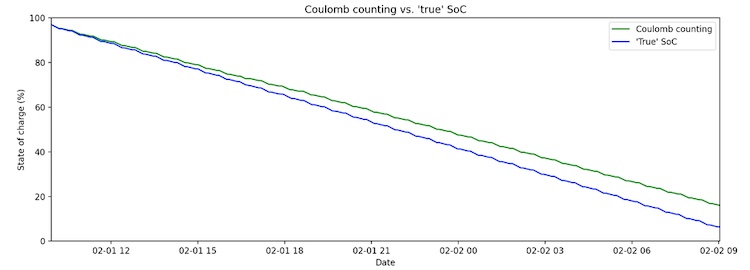
Coulomb counting can easily diverge from the true SoC between calibration points (full charge or discharge), even when the magnitude of error at each time step is very small.
Model-based approaches
There are two main routes under the model-based approach. The first is using an equivalent circuit model (ECM), most commonly the Thévenin model, to describe the electrical behavior of the battery. While this model does not perfectly describe the discharge behavior of the battery (especially at high output levels), it is a useful approximation and the resulting set of equations can be solved quickly and inexpensively.
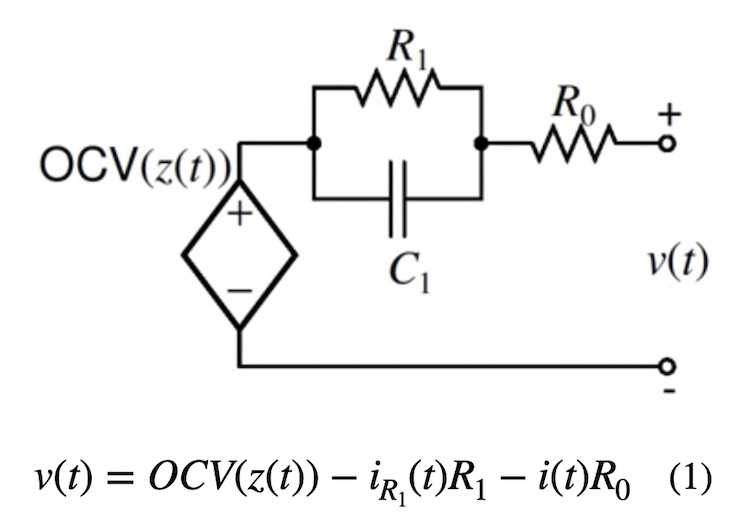
The Thévenin ECM is a tool that allows us to express the battery’s terminal voltage as a function of its open-circuit voltage (OCV) and voltages losses. Note that z(t) is the SoC at time t, and OCV is a function of SoC alone.
If greater accuracy is desired, the thermal-electrical battery model is experimentally accurate and derived from first principles. However, the resulting set of equations is much more computationally expensive to solve, and the improvement in accuracy compared to an ECM is marginal.
Data-driven approach
Finally, the data-driven approach uses machine learning models to map battery time-series data to SoC estimates. While this approach can be effective, it requires a large amount of labeled experimental data in order to train the model, and it can be challenging to ensure that the training data covers all use cases. Additionally, the model can be quite computationally expensive to run in real time.
Determining the best algorithm for our system
Our SoC algorithm must be both lightweight and accurate, especially when data could be spotty and we may see a wide range of user behavior and battery characteristics. Coulomb counting can only recalibrate at full charge, so during days of bad weather it’s likely that the algorithm would lose significant accuracy. On the other hand, a data-driven algorithm is too computationally expensive to run real time on our microcontroller (MCU), and it would take too long to collect the training data. From the remaining two model-based options, we choose the ECM approach, as simplicity and conservation of resources on our MCU are the priority over a slight tradeoff in accuracy.
The Algorithm
This article is about our implementation of a Kalman filter, which is essentially a tool used to predict a value and then update it based on a measurement. But why do we need to make predictions in this roundabout manner? Couldn’t we instead use the ECM voltage equation (1) to determine the SoC from the OCV? After all, OCV is a function of SoC, as shown in the mapping below.
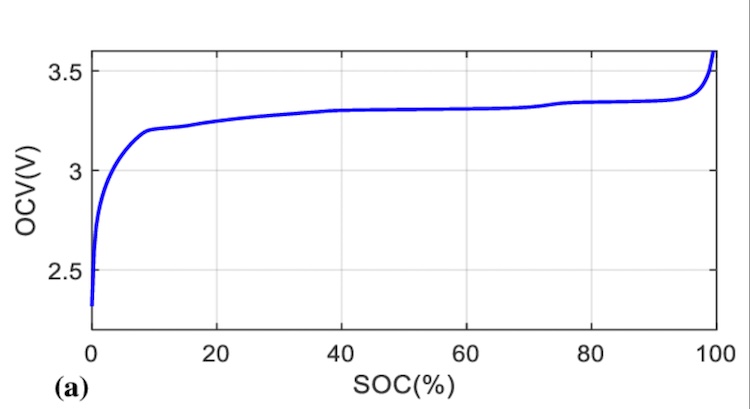
An OCV mapping from the literature is shown above. Note its nonlinearity as well as the flatness of the curve in the mid-range of SoC.
It turns out that we could do this, but the resulting SoC estimate would not be very accurate. This is due to approximations made in the ECM, noisy sensor data, and also the flatness of the OCV mapping in the 30-70% SoC region. The voltage hardly changes in this region, making it very difficult to extract an accurate SoC value from an OCV value. Even if the ECM voltage equation was a near perfect approximation (which it is not), it would be difficult to estimate SoC with confidence from an OCV value alone.
Therefore, the intention of the algorithm is to estimate SoC with the help of both the ECM and Coulomb counting, recursively updating and correcting our prediction with each new sensor value. In this way, the algorithm is essentially recalibrating the Coulomb counter at each time step. This adaptive structure of the Kalman filter makes the algorithm resilient to unpredictable or noisy data, gaps in data, or inaccurately initialized parameters.
Key steps in the algorithm
With each new sensor value received, several steps are taken to update the SoC estimate. First, we predict the new SoC value using the previous SoC value and measured current, as well as the time between updates. This is done using a Coulomb counter, as shown below. Note that Q represents the battery’s capacity.
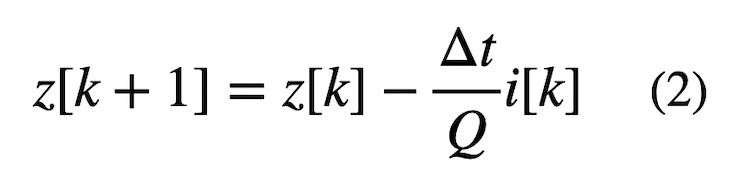
The Coulomb counter updates SoC (z) by accumulating the current entering or exiting the battery. The inaccuracies in this algorithm are mitigated with the corrective process in the Kalman Filter, effectively recalibrating the SoC at each time step.
Next, we feed this predicted SoC value into the Thévenin voltage equation (3), which defines a relationship between open circuit voltage (OCV), battery current, and terminal voltage (voltage of the battery while loaded) at time step k. This allows us to solve for the predicted battery terminal voltage, v[k], using our SoC prediction from the previous step.
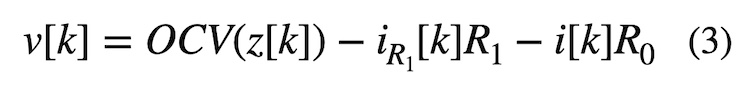
The discrete form of the ECM voltage output equation (3). Note the only difference from eqn (1) is that time k is a discrete valued time step rather than a continuous time value.
Now that we have a predicted battery voltage, we can use the battery voltage measurement as a point of reference. The Kalman filter enables us to analyze the error between the predicted and measured battery voltage and corrects the estimated SoC appropriately. This correction step sets the Kalman filter apart from other algorithms and provides an elegant solution to a difficult problem. Essentially, the Kalman filter uses the uncertainties in predicted and measured voltages to determine how much of an SoC correction is required. If there is large uncertainty in the predicted voltage, then the SoC will be largely determined by the measured voltage and vice versa.
Conditions necessary to apply a Kalman filter
To apply the Kalman filter, two assumptions must be satisfied:
1. The errors in battery current and voltage measurements are independent and Gaussian
2. Both the SoC update equation (2) and ECM voltage equation (3) must be linear
We can safely assume the first, but not the second. As shown earlier, the OCV → SoC mapping is nonlinear, making the ECM voltage equation nonlinear. So the final piece of the algorithm is to make a linear approximation of this equation, using the Extended Kalman Filter (EKF). This approximation is done using a first-order Taylor series expansion, which yields a linear approximation about a single point. Using this approximation, the EKF follows the same steps as the linear Kalman filter in order to simply compare the predicted voltage value to the measured voltage, calculate an error term, and correct the SoC accordingly. The next step is to observe its performance and determine how to optimize the algorithm going forward.
Testing the algorithm
In order to tune the Kalman filter and evaluate its accuracy, we completely discharged a battery using current pulses of varying intensity. When we calculated the final SoC (using the final resting voltage as our OCV) and summed up the total load drawn from the battery over the course of the experiment, the battery capacity turned out to be ~80% of the rated capacity. The Kalman filter’s feedback loop is adaptive, but it is still difficult to overcome such a large discrepancy in a parameter as critical as battery capacity. We see that with the battery capacity set at the rated capacity, the Kalman SoC estimate slowly diverges from the true SoC until it is able to sync up at ~15% SoC as the battery’s voltage dissipates.
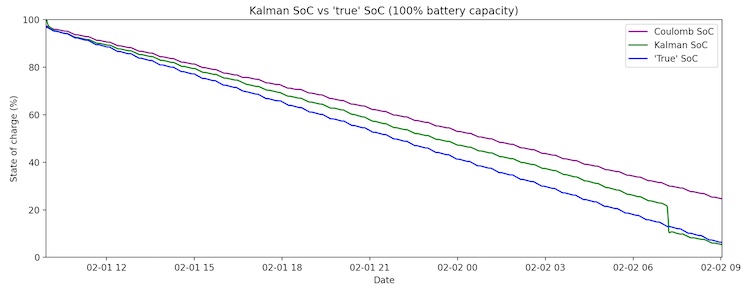
With battery capacity set at the rated capacity, the Kalman filter’s adaptivity enables it to perform far better than Coulomb counting.
While it is encouraging that the SoC syncs up with the true value eventually and performs significantly better than a Coulomb counter (5% root mean squared error compared to over 11%), we would like to improve our accuracy further. In order to do this, we adjust the battery capacity to line up more closely with reality. Using 85% of the rated battery capacity, we find that the Kalman SoC lines up almost exactly with the expected SoC.
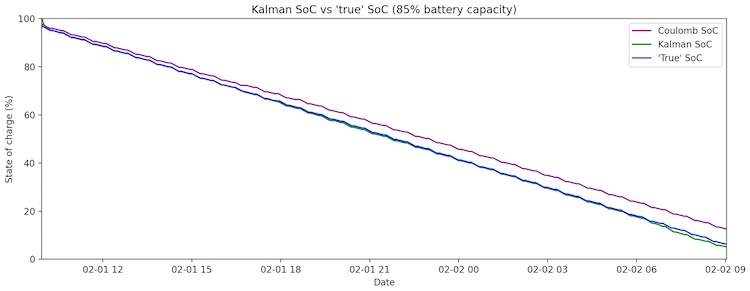
After decreasing the battery capacity to 85% of the rated capacity, we were able to estimate SoC with less than 1% RMSE for a single discharge with the Kalman filter.
Interestingly, when we decrease the battery capacity to 80% of its rating, the Coulomb counter tracks the expected SoC almost exactly, but the Kalman SoC slightly underestimates until it syncs up at the end of the discharge. This is likely a consequence of not including a hysteresis term in the ECM voltage equation, which causes the Kalman filter to slightly overestimate the battery voltage, leading to a negative SoC correction. In the future, we plan to add hysteresis to our ECM in order to further optimize performance.
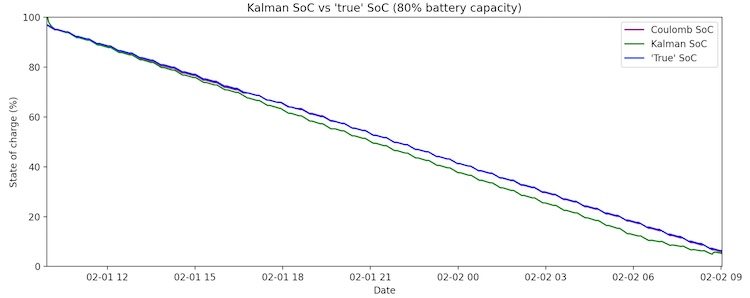
After decreasing the battery capacity to 80% of the rated capacity, the Coulomb SoC tracks the true SoC almost exactly and the Kalman diverges slightly.
Ultimately, both Coulomb counting and the Kalman filter perform well when the battery capacity is accurate. The difference is that the Kalman filter can handle a wide range of parameter errors and, in the case of a data outage, adapts and quickly re-converges to the true SoC value while the Coulomb counter would be lost until it reaches a recalibration point.
Next Steps
At this stage we are confident enough in our lab results and are currently deploying this algorithm to the field, where battery usage and health will vary widely, and we will collect more data to inform future improvements. Already we plan to build an adaptive battery capacity into the Kalman filter, so we can stop relying on the inaccurate rated capacities, improve our SoC accuracy, and track battery health across our networks. Stay tuned for future updates on how this algorithm progresses and also how this algorithm is used to support new product features, coming soon!
Acknowledgements
- University of Colorado’s Battery SoC Estimation online course – This is what finally gave me an intuition for how a Kalman filter works after a lot of getting nowhere through other sources
OCV mapping figures



